- Autor Matthew Elmers [email protected].
- Public 2023-12-16 21:57.
- Zadnja izmjena 2025-01-24 09:20.

Šta određuje tačnost - jednu od glavnih karakteristika oružja? Očigledno, od kvalitete cijevi i patrone. Odložimo uložak za sada, ali razmotrimo fiziku procesa.
Uzmite metalnu šipku ili cijev od elastičnog metala i čvrsto je učvrstite u masivnu podlogu. Tako smo dobili model uređaja koji se proučava. Sada, ako pogodimo štap, nije važno na kojem mjestu i u kojem smjeru, ili ga povući unatrag, ili ga stisnuti, ili, konačno, umetanjem patrone u cijev i ispaljivanjem hica, vidjet ćemo da štap (cijev) došlo je do prigušenog oscilatornog kretanja. Ove vibracije se razlažu na najjednostavnije, a svaka vrsta tako jednostavne vibracije cijevi će na svoj način uticati na tačnost (tačnost) gađanja.
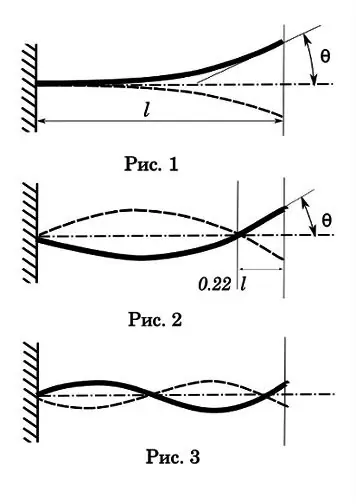
Počnimo s vibracijama prvog reda ili visine. Kao što vidite (slika 1), takva oscilacija ima samo jedan čvor u tački vezivanja, najveću amplitudu, najduže vrijeme opadanja i najduže vrijeme oscilacije u jednom periodu. Ovo vrijeme je 0,017-0,033 sek. Vrijeme putovanja metka kroz provrt je 0, 001-0, 002 sek. Odnosno, znatno manje od ciklusa jedne oscilacije, što znači da ova vrsta oscilacija nema značajan utjecaj na preciznost jednog udarca. No s automatskim snimanjem može se pojaviti zanimljiva slika. Recimo da je brzina paljbe 1200 o / min, tj. vrijeme jednog ciklusa - 0,05 sek. Sa periodom oscilacija prvog reda od 0, 025 sek, imamo omjer više frekvencija. A ovo je neizostavan uvjet za rezonanciju sa svim posljedicama koje slijede - oružje počinje tresti takvom snagom da se može raspasti.
Prijeđimo na oscilacije drugog reda (slika 2). Ali predlažem da studenti humanističkih nauka prvo provedu eksperiment kako bi otklonili nedostatke obrazovanja u oblasti fizike. Morate uzeti malog dječaka (možete i djevojčicu), staviti ga na ljuljačku i ljuljati se. Pred vama je klatno. Stanite sa strane ljuljačke i pokušajte udariti dječaka loptom. Nakon niza pokušaja, doći ćete do zaključka da je najbolji način pogađanja kada je meta u prvoj fazi oscilacije - maksimalno odstupanje od točke ravnoteže. U ovom trenutku cilj ima nultu brzinu.
Pogledajmo dijagram drugog reda. Drugi čvor vibracija nalazi se približno 0,22 od kraja cijevi. Ova točka je zakon prirode, nemoguće je stvoriti takve vibracije za konzolnu gredu tako da drugi čvor padne na slobodni kraj. Tu se nalazi i ne zavisi od dužine cijevi.
Amplituda oscilacija za šemu drugog reda je manja, ali je vrijeme oscilacije već uporedivo s vremenom prolaska metka kroz provrt-0, 0025-0, 005 sek. Dakle, za pojedinačno snimanje ovo je već od interesa. Da bi bilo jasno o čemu govorimo, zamislite bure dugačko 1 metar. Metak prolazi kroz cijelu cijev za 0,001 sekundi. Ako je period oscilacije 0,004 sek, tada će do trenutka kada metak napusti cijev, cijev u prvoj fazi dostići svoj maksimalni zavoj. Pitanje za humanističke nauke je - u kojem je trenutku (u kojoj fazi) najbolje ispaliti metak iz cijevi kako bi se osigurala konzistentnost rezultata? Upamti zamah. U nultoj točki, vektor brzine skretanja debla je maksimalan. Metak je teže pogoditi ovu točku na rezu cijevi, također ima svoju grešku u brzini. Odnosno, najbolji trenutak za izlijetanje metka bit će kada je cijev na najvišoj točki prve faze skretanja - kao na slici. Tada će se neznatna odstupanja u brzini metka kompenzirati duljim vremenom koje je cijev provela u svojoj najstabilnijoj fazi.
Grafički prikaz ove pojave može se jasno vidjeti na dijagramu (slika 4-5). Ovdje - Δt je vremenska greška s kojom metak prelazi cijev cijevi. Na sl. 4 je idealno kada se prosječno vrijeme uzlijetanja metka podudara s nultom fazom oscilacija cijevi. (Matematičari! Znam da je raspodjela brzine nelinearna.) Osjenčano područje je kut širenja trajektorija.
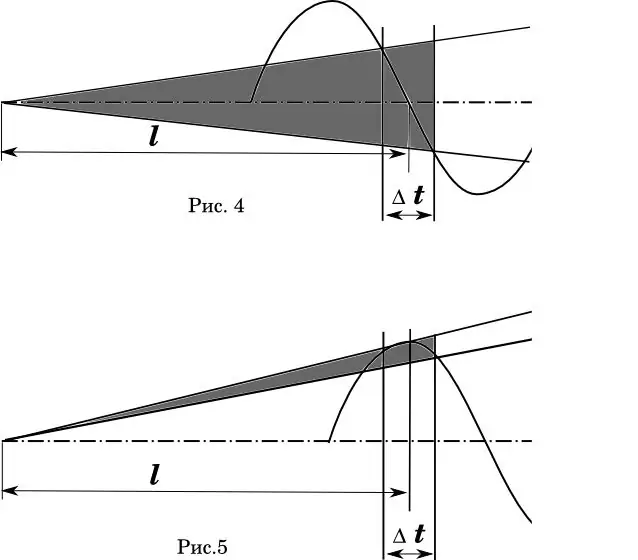
Na slici 5, dužina cijevi i greška brzine ostaju iste. No, faza savijanja cijevi se pomiče tako da se prosječno vrijeme polaska podudara s maksimalnim otklonom cijevi. Jesu li komentari suvišni?
Pa, je li vrijedno svijeće? Koliko odstupanja uzrokovana oscilacijama drugog reda mogu biti ozbiljna? Ozbiljno i vrlo ozbiljno. Prema sovjetskom profesoru Dmitriju Aleksandroviču Ventzelu, u jednom od eksperimenata postignuti su sljedeći rezultati: radijus srednjeg odstupanja povećao se za 40% s promjenom dužine cijevi za samo 100 mm. Za usporedbu, visokokvalitetna obrada cijevi može poboljšati točnost za samo 20%!
Pogledajmo sada formulu za frekvenciju vibracije:
gdje:
k - koeficijent oscilacija drugog reda - 4, 7;
L je dužina cijevi;
E je modul elastičnosti;
I je moment inercije presjeka;
m je masa debla.
… i nastavite s analizom i zaključcima.
Očigledan zaključak sa slika 4-5 je greška brzine metka. Ovisi o kvaliteti praha i njegovoj težini i gustoći u ulošku. Ako je ova greška najmanje četvrtina ciklusa, tada se može odustati od svega ostalog. Srećom, nauka i industrija postigle su vrlo veliku stabilnost po ovom pitanju. A za sofisticiranije (na primjer u bensteretu) postoje svi uvjeti za samostalno sastavljanje patrona kako bi se faza oslobađanja metka prilagodila točno dužini cijevi.
Dakle, imamo uložak s najmanjom mogućom varijacijom brzine. Dužina cijevi je izračunata na osnovu maksimalne težine. Postavlja se pitanje stabilnosti. Posmatramo formulu. Koje varijable utječu na promjenu frekvencije oscilacija? Dužina cijevi, modul elastičnosti i masa. Cijev se zagrijava tokom pucanja. Može zagrijati promjenu dužine cijevi tako da se utiče na tačnost. Da i ne. Da, budući da je ta brojka unutar stotih postotaka za temperaturu od 200 C. Ne, budući da je promjena modula elastičnosti čelika za istu temperaturu oko 8-9%, za 600C to je gotovo dvostruko. Odnosno, mnogo puta veći! Cijev postaje mekša, faza savijanja cijevi se pomiče prema naprijed onog trenutka kad metak izađe, tačnost pada. Pa, šta kaže pažljivi analitičar? Reći će da je nemoguće postići maksimalnu tačnost na jednoj cijevi u hladnom i vrućem načinu rada! Oružje bi moglo imati bolje performanse sa hladnom ili vrućom cijevi. U skladu s tim dobivaju se dvije klase oružja. Jedan je za akcije zasjede, kada se cilj mora pogoditi iz prvog - "hladnog" hica, jer će tačnost drugog biti lošija zbog neizbježnog zagrijavanja cijevi. U takvom oružju nema hitne potrebe za automatizacijom. I druga klasa su automatske puške, čija je dužina cijevi prilagođena vrućoj cijevi. U ovom slučaju, mogući promašaj zbog niske preciznosti hladnog udarca može se nadoknaditi brzim naknadnim vrućim i preciznijim udarcem.
EF Dragunov je vrlo dobro poznavao fiziku ovog procesa dok je dizajnirao svoju pušku. Predlažem da se upoznate s pričom o njegovom sinu Alekseju. Ali prvo će neko morati razbiti mozak. Kao što znate, dva uzorka Konstantinova i Dragunova približila su se finalu takmičenja za snajpersku pušku. Dizajneri su bili prijatelji i pomagali jedni drugima u svemu. Dakle, Konstantinova puška je "podešena" na hladni način rada, Dragunovljeva puška na "vruću". Pokušavajući poboljšati preciznost suparničke puške, Dragunov puca puškom s dugim pauzama.

Pogledajmo formulu ponovo. Kao što vidite, učestalost ovisi i o masi cijevi. Masa prtljažnika je konstantna. Ali čvrst kontakt sa čelom proizvodi nepredvidljive pozitivne povratne informacije o cijevi. Sistem-cijev-prednji krak (nosač) imat će drugačiji moment inercije (skup masa u odnosu na točku pričvršćivanja), što znači da i to može uzrokovati fazni pomak. Zbog toga sportaši koriste meku podršku. Ista značajka povezana je s primjenom načela "viseće cijevi", kada čelo oružja nema čvrst kontakt sa cijevi i kruto je pričvršćeno za njega (oružje) samo u području prijemnik, a drugi kraj ili uopće ne dodiruje cijev ili dodiruje spoj sa oprugom (SVD).
Završna misao. Činjenica da je s istom dužinom cijevi nemoguće postići istu točnost na različitim temperaturama daje odličan razlog za rastezanje mozga. Samo je potrebno promijeniti dužinu i / ili masu cijevi kada se promijeni temperatura cijevi. Bez promjene niti dužine niti težine cijevi. Sa gledišta humanističkih nauka, ovo je paradoks. Sa stajališta tehničara, idealan zadatak. Cijeli život dizajnera povezan je s rješavanjem takvih problema. Šerloci se odmaraju.






